 and its Fourier transform
and its Fourier transform  :
:
First I will provide my own favorite definition of a continuous wavelet transform, which I wrote down in 1986 to rederive the results in Goupillaud et al [1]. (At the time, I was working down the hall from Pierre Goupillaud.) This continuous transform seemed much better suited to geophysical and acoustic applications than certain discrete transforms popular at the time, particularly Daubechies wavelets. Many wavelets have a broader spectrum than necessary, more suitable for compressing photographic images with sharp edges. A continuous transform can use simple Gaussian tapered monochromatic waves (one or multi-dimensional) which maximizes the locality in both time/space and frequency/wavenumber.
First, I will give the definition of what constitutes a valid “wavelet” for the transform. Second, the inverse of a wavelet transform will be derived to demonstrate why the transform works. Next, I will show how a wavelet-transform of a stretched function can be written as a simple function of the wavelet-transform of the original unstretched function. Such stretching is very useful in pseudo-spectral solutions of differential equations with spatially varying coefficients.
Next I dwell on the original Morlet wavelet, a Gaussian-tapered sinusoid, to show how resolution can be managed explicitly in both time and frequency domains.
(This is an expansion of a much older document [2] that stressed the application of wavelet transforms to seismic imaging. I have removed the geophysical details and have extended the discussion.)
I will closely imitate the continuous transform originally provided by Goupillaud, Grossman, and Morlet [1]. They provide forward and inverse transforms for related transforms, but without derivation.
Use the following Fourier convention to link a
wavelet 

The following integral must exist for a wavelet to be suitable for a continuous transform over all frequencies.
 (3)
(3)

 as
as
 for some
for some  .
.
In fact many useful wavelets (such as the Morlet wavelet) will be non-zero at zero frequency and will not be valid for an infinite range of frequencies. Discrete transforms will prefer damped least-squares optimizations rather than simple integrals for transformations and will not require an analytic constant for normalization.
This wavelet need not correspond to any specific feature in our data. Rather, when convolved with data, the wavelet should suppress all but a band of frequencies. Because of the uncertainty principle, I must balance the narrowness of the bandwidth with the narrowness in time.
I recommend a Gaussian-tapered sinusoid, such as


A valid wavelet can be used in an unfamiliar construction of a delta function.
In effect, this integral says that many wavelets, stretched uniformly over all scales, will sum destructively everywhere but at .
.
 (5)
(5)
 to
to  .
The Jacobian is
.
The Jacobian is
 .
Thus,
.
Thus,
 |
 |
 |
(6) |
 |
 |
(7) | |
 |
 |
(8) | |
 |
 |
(9) |
The constraint of symmetry will also simplify the definition of a wavelet transform in the following section, but this assumption is optional:
 (10)
(10)
Define a wavelet transform 


 and local frequency
and local frequency  . When calculated
discretely, the sampling need not be uniform over
. When calculated
discretely, the sampling need not be uniform over  and
and  ,
but the weights should reflect the above integration.
,
but the weights should reflect the above integration.
Goupillaud et all
[1] prefer 


I find the following inverse, which simply scales and sums the transform
with uniform weight over local frequency 
 |
 |
![$\displaystyle C_w^{-1} \int \left \{ \int w[u(t - t' )] f(t') dt' \right \} du$](img39.svg) |
(13) |
 |
![$\displaystyle C_w^{-1} \int \left \{ \int w[u(t - t' )] du \right \} f(t') dt'$](img40.svg) |
(14) | |
 |
 |
(15) | |
 |
 |
(16) |
Most all these equations were implicit in Goupillaud et al [1], although I personally found it nontrivial to fill in the missing derivation of the results. I was also happy to stumble on equation (4), which continues to fascinate me.
One application that frequently appears is a differential stretching of a function.
We will write
![$\displaystyle g(\tau) = f[t(\tau)].
$](img43.svg) (17)
(17)
 gives the input coordinate
gives the input coordinate  as a monotonically increasing
function of the output coordinate
as a monotonically increasing
function of the output coordinate  .
Moreover, I will assume that the stretching
function can be well approximated locally by a straight line.
.
Moreover, I will assume that the stretching
function can be well approximated locally by a straight line.
 with the same wavelets as in definition (11)
and inverse (12).
with the same wavelets as in definition (11)
and inverse (12).
![$\displaystyle G(v, b ) = \int w [ v ( b - \tau ) ] g (\tau) d\tau ~~~~ {\rm and}
$](img53.svg) (20)
(20)
 (21)
(21)
 as a simple function of
as a simple function of  . The approximation (18)
allows us to write
We can perform an equivalent stretch on the transformed
input by stretching the position
. The approximation (18)
allows us to write
We can perform an equivalent stretch on the transformed
input by stretching the position  , and by scaling
the local frequency
, and by scaling
the local frequency  . Both operations require a simple
two-dimensional mapping of the transformed function.
The amplitude must be scaled as well.
. Both operations require a simple
two-dimensional mapping of the transformed function.
The amplitude must be scaled as well.
 |
 |
![$\displaystyle \int w[v(b-\tau)] \cdot f[t(\tau)] d \tau$](img58.svg) |
(23) |
 |
![$\displaystyle \int w [ v(b-\tau)] \cdot f \left [ t(b) + (\tau-b)
\cdot {dt \over d\tau} ( b ) \right ] d\tau \ldots$](img59.svg) |
(24) |
 |
 |
 |
(25) |
 |
 |
![$\displaystyle b + [ t' - t(b) ]
\cdot \left [ {dt \over d\tau} ( b ) \right ]^{-1} .$](img64.svg) |
(26) |
 |
 |
![$\displaystyle \int w \left \{ v \cdot [t(b) - t'] \cdot
\left [ {dt \over d\tau...
...\} \cdot f(t')
\cdot \left \vert {dt \over d\tau} ( b ) \right \vert^{-1} ~ dt'$](img66.svg) |
(27) |
 |
![$\displaystyle \left \vert {dt \over d\tau} ( b ) \right \vert^{-1}
\int w \left...
...t \over d\tau} ( b ) \right ]^{-1}
\cdot [t(b) - t']
\right \} \cdot f(t') d t'$](img67.svg) |
(28) | |
 |
![$\displaystyle \left \vert {dt \over d\tau} ( b ) \right \vert^{-1}
~ F \left \{ u=v \cdot
\left [ {dt \over d\tau} ( b ) \right ]^{-1} , ~ a = t(b) \right \} .$](img68.svg) |
(29) |
 was not necessary here.
was not necessary here.
Equation (22) is the result which allows us to perform the stretch directly on the wavelet-transformed function.
A preferred standard wavelet is the Morlet wavelet
[1], constructed from a symmetric cosine tapered by a Gaussian.
 |
 |
 |
(30) |
 |
 |
 |
(31) |
 |
 |
 |
(32) |
 |
 |
 |
(33) |
 and
and  do not vary during a wavelet transform.
If we take the dimension
do not vary during a wavelet transform.
If we take the dimension  as units of time in seconds,
then
as units of time in seconds,
then  is the central frequency of the wavelet in hertz.
The “half-width”
is the central frequency of the wavelet in hertz.
The “half-width”  controls the relative width of the taper in wavelengths.
controls the relative width of the taper in wavelengths.
The cosine has a base frequency of 





The envelope has a peak value of 1 at 

 |
 |
 |
(34) |
![$\displaystyle m_g[h/(2 \bar{s})]$](img82.svg) |
 |
![$\displaystyle m_g[-h/(2 \bar{s})]$](img83.svg) |
(35) |
 |
 |
(36) |
 the half-width, in wavelengths, of the Gaussian taper.
the half-width, in wavelengths, of the Gaussian taper.
The integral of the Gaussian envelope in time 
 |
(37) |
As an example, figure 1 shows one Morlet wavelet.
We assume a time sampling interval of 







We can take the Fourier transform (1) of the Gaussian envelope as
 ,
approximately spanning the range of values more than half of the peak value.
This half-width
,
approximately spanning the range of values more than half of the peak value.
This half-width  in units of frequency is just the reciprocal of the
half-width
in units of frequency is just the reciprocal of the
half-width  in units of time.
in units of time.
Notice that the frequency half-width is directly proportional to the reference frequency 
The Fourier transform of the cosine is
 |
 |
 |
(40) |
 |
 |
(41) |
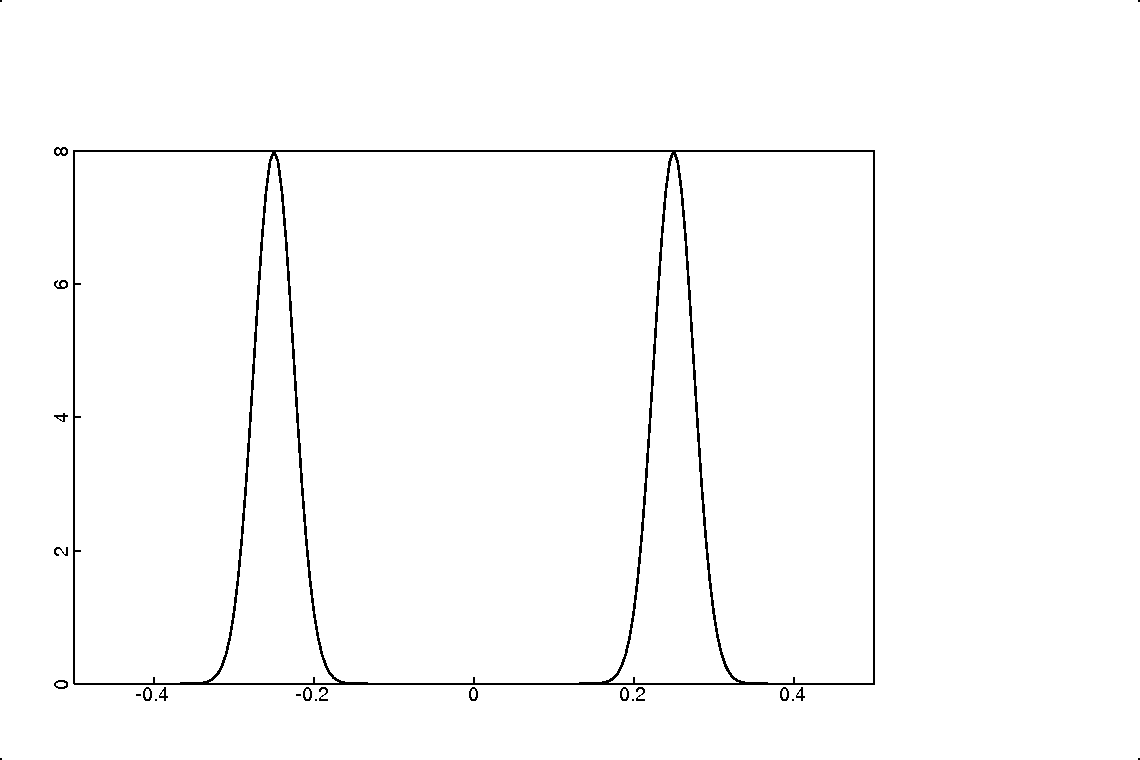
Figure 2 shows the Fourier transform of the Morlet wavelet in figure 1,
also with 

|
The resolution we care about is the narrowness of the spectrum about the central frequency 
For quantifying resolution tradeoffs, a useful measure is the normalized second moment, or dispersion, in each domain.
In time, the integral of the squared Gaussian taper is
 |
(45) |
 |
(46) |
 |
 |
 |
(47) |
 |
 |
 |
(48) |
Similarly we can measure second moments in the frequency domain.
 |
 |
 |
(49) |
 |
 |
 |
(50) |
The uncertainty relation for resolution in time and frequency simplifies to
 |
(51) |
 and the central frequency
and the central frequency  .
The half-width in wavelengths
.
The half-width in wavelengths  controls the width of resolution in each domain,
but cannot change this product of two widths.
Improving the resolution in one domain necessarily reduces the resolution in the other.
If we double the width of the envelope in the time domain, then we necessarily halve
the width in the frequency domain.
controls the width of resolution in each domain,
but cannot change this product of two widths.
Improving the resolution in one domain necessarily reduces the resolution in the other.
If we double the width of the envelope in the time domain, then we necessarily halve
the width in the frequency domain.